\(\text{12,56637061...}\)
Mark off the required number of decimal places: \(\text{12,566}|37061\ldots\). The next digit is a \(\text{3}\) and so we round down: \(\text{12,566}\).
|
Previous
1.3 Rational and irrational numbers
|
Next
1.5 Estimating surds
|
Rounding off a decimal number to a given number of decimal places is the quickest way to approximate a number. For example, if you wanted to round off \(\text{2,6525272}\) to three decimal places, you would:
count three places after the decimal and place a \(|\) between the third and fourth numbers;
round up the third digit if the fourth digit is greater than or equal to \(\text{5}\);
leave the third digit unchanged if the fourth digit is less than \(\text{5}\);
if the third digit is \(\text{9}\) and needs to be rounded up, then the \(\text{9}\) becomes a \(\text{0}\) and the second digit is rounded up.
So, since the first digit after the \(|\) is a \(\text{5,}\) we must round up the digit in the third decimal place to a \(\text{3}\) and the final answer of \(\text{2,6525272}\) rounded to three decimal places is \(\text{2,653}\).
The following video explains how to round off.
Round off the following numbers to the indicated number of decimal places:
\(\dfrac{120}{99}=\text{1,}\dot{2}\dot{1}\) to \(\text{3}\) decimal places.
\(\pi =\text{3,141592653...}\) to \(\text{4}\) decimal places.
\(\sqrt{3}=\text{1,7320508...}\) to \(\text{4}\) decimal places.
\(\text{2,78974526}\) to \(\text{3}\) decimal places.
If the number is not a decimal you first need to write the number as a decimal.
\(\dfrac{120}{99} = \text{1,212}|121212\ldots\)
\(\pi =\text{3,1415}|92653\ldots\)
\(\sqrt{3}=\text{1,7320}|508\ldots\)
\(\text{2,789}|74526\)
The last digit of \(\frac{120}{99}=\text{1,212}|121212\dot{1}\dot{2}\) must be rounded down.
The last digit of \(\pi =\text{3,1415}|92653\ldots\) must be rounded up.
The last digit of \(\sqrt{3}=\text{1,7320}|508\ldots\) must be rounded up.
The last digit of \(\text{2,789}|74526\) must be rounded up.
Since this is a \(\text{9}\) we replace it with a \(\text{0}\) and round up the second last digit.
\(\dfrac{120}{99}=\text{1,212}\) rounded to \(\text{3}\) decimal places.
\(\pi =\text{3,1416}\) rounded to \(\text{4}\) decimal places.
\(\sqrt{3}=\text{1,7321}\) rounded to \(\text{4}\) decimal places.
\(\text{2,790}\)
Round off the following to \(\text{3}\) decimal places:
\(\text{12,56637061...}\)
Mark off the required number of decimal places: \(\text{12,566}|37061\ldots\). The next digit is a \(\text{3}\) and so we round down: \(\text{12,566}\).
\(\text{3,31662479...}\)
Mark off the required number of decimal places: \(\text{3,316}|62479\ldots\). The next digit is a \(\text{6}\) and so we round up: \(\text{3,317}\).
\(\text{0,2666666...}\)
Mark off the required number of decimal places: \(\text{0,266}|6666\ldots\). The next digit is a \(\text{6}\) and so we round up: \(\text{0,267}\).
\(\text{1,912931183...}\)
Mark off the required number of decimal places: \(\text{1,912}|931183\ldots\). The next digit is a \(\text{9}\) and so we round up: \(\text{1,913}\).
\(\text{6,32455532...}\)
Mark off the required number of decimal places: \(\text{6,324}|55532\ldots\). The next digit is a \(\text{5}\) and so we round up: \(\text{6,325}\).
\(\text{0,05555555...}\)
Mark off the required number of decimal places: \(\text{0,055}|55555\ldots\). The next digit is a \(\text{5}\) and so we round up: \(\text{0,056}\).
Round off each of the following to the indicated number of decimal places:
\(\text{345,04399906}\) to \(\text{4}\) decimal places.
\[\text{345,04399906} \approx \text{345,0440}\]
\(\text{1 361,72980445}\) to \(\text{2}\) decimal places.
\[\text{1 361,72980445} \approx \text{1 361,73}\]
\(\text{728,00905239}\) to \(\text{6}\) decimal places.
\[\text{728,00905239} \approx \text{728,009052}\]
\(\dfrac{1}{27}\) to \(\text{4}\) decimal places.
We first write the fraction as a decimal and then we can round off.
\begin{align*} \frac{1}{27} &= \text{0,037037...} \\ & \approx \text{0,0370} \end{align*}\(\dfrac{45}{99}\) to \(\text{5}\) decimal places.
We first write the fraction as a decimal and then we can round off.
\begin{align*} \frac{45}{99} &= \text{0,45454545...} \\ & \approx \text{0,45455} \end{align*}\(\dfrac{1}{12}\) to \(\text{2}\) decimal places.
We first write the fraction as a decimal and then we can round off.
\begin{align*} \frac{1}{12} &= \text{0,08333...} \\ & \approx \text{0,08} \end{align*}Study the diagram below
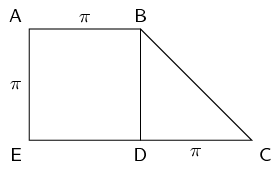
Calculate the area of \(ABDE\) to \(\text{2}\) decimal places.
\(ABDE\) is a square and so the area is just the length squared.
\begin{align*} A &= l^{2} \\ &= \pi^2 \\ & = \text{9,86904...} \\ & \approx \text{9,87} \end{align*}Calculate the area of \(BCD\) to \(\text{2}\) decimal places.
\(BCD\) is a right-angled triangle and so we have the perpendicular height. The area is:
\begin{align*} A & = \frac{1}{2} b h\\ & = \frac{1}{2} \pi^2 \\ & = \text{4,934802...} \\ & \approx \text{4,93} \end{align*}Using you answers in (a) and (b) calculate the area of \(ABCDE\).
The area of \(ABCDE\) is the sum of the areas of \(ABDE\) and \(BCD\).
\begin{align*} A & = \text{9,87} + \text{4,93} \\ & \approx \text{14,80} \end{align*}Without rounding off, what is the area of \(ABCDE\)?
Given \(i = \dfrac{r}{600}\); \(r = \text{7,4}\); \(n = 96\); \(P = \text{200 000}\).
Calculate \(i\) correct to \(\text{2}\) decimal places.
Using you answer from (a), calculate \(A\) in \(A = P(1+ i)^n\).
Calculate \(A\) without rounding off your answer in (a), compare this answer with your answer in (b).
There is a \(\text{128 913,63}\) difference between the answer in (b) and the one calculated without rounding until the final step.
If it takes \(\text{1}\) person to carry \(\text{3}\) boxes, how many people are needed to carry \(\text{31}\) boxes?
Each person can carry 3 boxes. So we need to divide 31 by 3 to find out how many people are needed to carry 31 boxes.
\[\frac{31}{3} = \text{10,3333...}\]Therefore \(\text{11}\) people are needed to carry \(\text{31}\) boxes. We cannot have \(\text{0,333}\) of a person so we round up to the nearest whole number.
If \(\text{7}\) tickets cost \(\text{R}\,\text{35,20}\), how much does one ticket cost?
Since 7 tickets cost \(\text{R}\,\text{35,20}\), 1 ticket must cost \(\text{R}\,\text{35,20}\) divided by 7.
\[\frac{\text{35,20}}{7} =\text{5,028571429}\\\]Therefore one ticket costs \(\text{R}\,\text{5,03}\). Money should be rounded off to \(\text{2}\) decimal places.
|
Previous
1.3 Rational and irrational numbers
|
Table of Contents |
Next
1.5 Estimating surds
|