Show that if \(a<0\), then the range of \(f(x)=a{\left(x+p\right)}^{2}+q\) is \(\left\{f(x):f(x)\in \left(-\infty ,q\right]\right\}\).
End of chapter exercises
|
Previous
5.8 Summary
|
Next
6.1 Revision
|
End of chapter exercises
If \(\left(2;7\right)\) is the turning point of \(f(x)=-2{x}^{2}-4ax+k\), find the values of the constants \(a\) and \(k\).
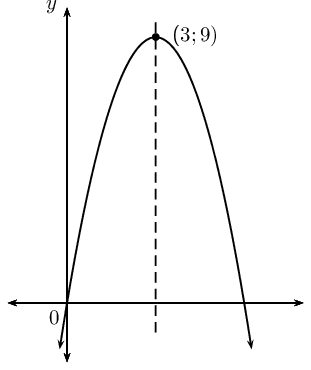
The following graph is represented by the equation \(f(x)=a{x}^{2}+bx\). The coordinates of the turning point are \(\left(3;9\right)\). Show that \(a=-1\) and \(b=6\).
Given: \(f(x)={x}^{2}-2x+3\). Give the equation of the new graph originating if:
the graph of \(f\) is moved three units to the left.
the \(x\)-axis is moved down three units.
A parabola with turning point \(\left(-1;-4\right)\) is shifted vertically by \(\text{4}\) units upwards. What are the coordinates of the turning point of the shifted parabola?
Plot the graph of the hyperbola defined by \(y=\frac{2}{x}\) for \(-4\le x\le 4\). Suppose the hyperbola is shifted \(\text{3}\) units to the right and \(\text{1}\) unit down. What is the new equation then?
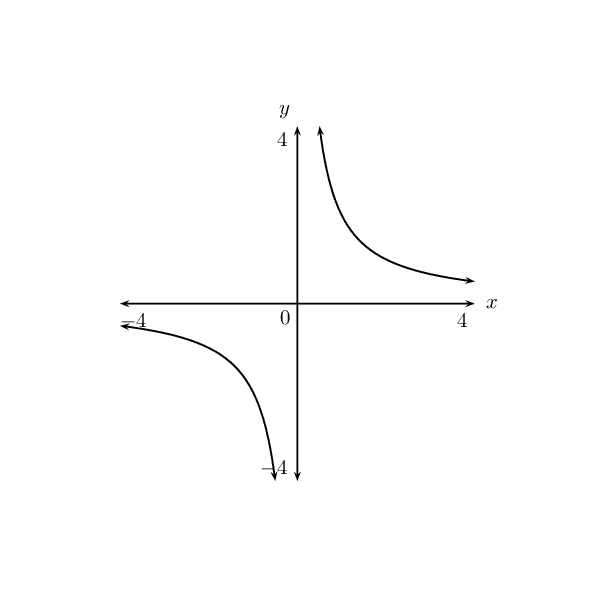
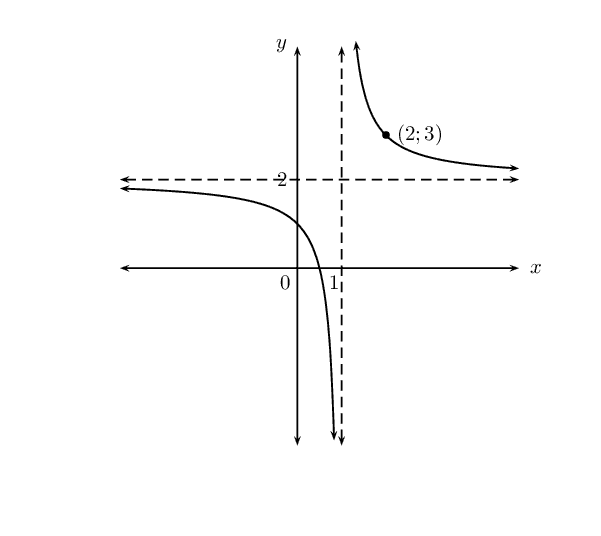
Based on the graph of \(y=\frac{k}{(x+p)} + q\), determine the equation of the graph with asymptotes \(y=2\) and \(x=1\) and passing through the point \(\left(2;3\right)\).
The columns in the table below give the \(y\)-values for the following functions: \(y={a}^{x}\), \(y={a}^{x+1}\) and \(y={a}^{x}+1\). Match each function to the correct column.
| \(x\) | A | B | C |
| \(-\text{2}\) | \(\text{7,25}\) | \(\text{6,25}\) | \(\text{2,5}\) |
| \(-\text{1}\) | \(\text{3,5}\) | \(\text{2,5}\) | \(\text{1}\) |
| \(\text{0}\) | \(\text{2}\) | \(\text{1}\) | \(\text{0,4}\) |
| \(\text{1}\) | \(\text{1,4}\) | \(\text{0,4}\) | \(\text{0,16}\) |
| \(\text{2}\) | \(\text{1,16}\) | \(\text{0,16}\) | \(\text{0,064}\) |
Column A: \(y={a}^{x} + 1\); Column B: \(y={a}^{x}\); Column C: \(y={a}^{x + 1}\)
The graph of \(f(x) = 1 + a \cdot 2^x\) (\(a\) is a constant) passes through the origin.
Determine the value of \(a\).
Determine the value of \(f(-15)\) correct to five decimal places.
Determine the value of \(x\), if \(P\left(x;\text{0,5}\right)\) lies on the graph of \(f\).
If the graph of \(f\) is shifted \(\text{2}\) units to the right to give the function \(h\), write down the equation of \(h\).
The graph of \(f(x) = a \cdot b^x\) (\(a ≠ 0\)) has the point \(P\left(2;\text{144}\right)\) on \(f\).
If \(b = \text{0,75}\), calculate the value of \(a\).
Hence write down the equation of \(f\).
Determine, correct to two decimal places, the value of \(f(13)\).
Describe the transformation of the curve of \(f\) to \(h\) if \(h(x)=f(-x)\).
Using your knowledge of the effects of \(p\) and \(k\) draw a rough sketch of the following graphs without a table of values.
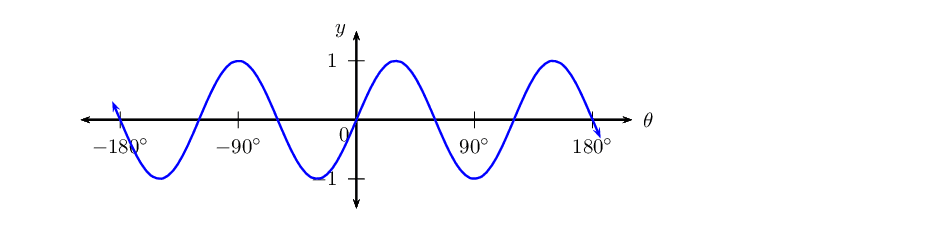
\(y = \sin 3\theta\) for \(-\text{180}\text{°} \leq \theta \leq \text{180}\text{°}\)
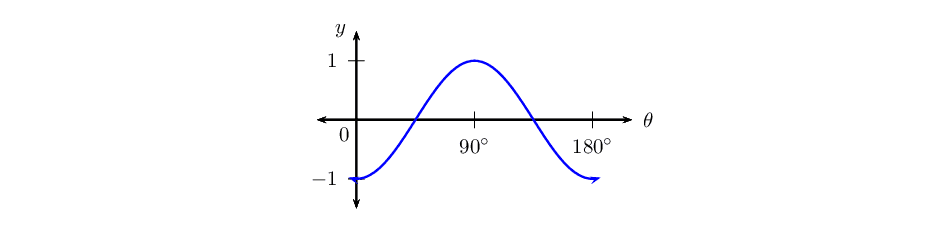
\(y = -\cos 2\theta\) for \(\text{0}\text{°} \leq \theta \leq \text{180}\text{°}\)
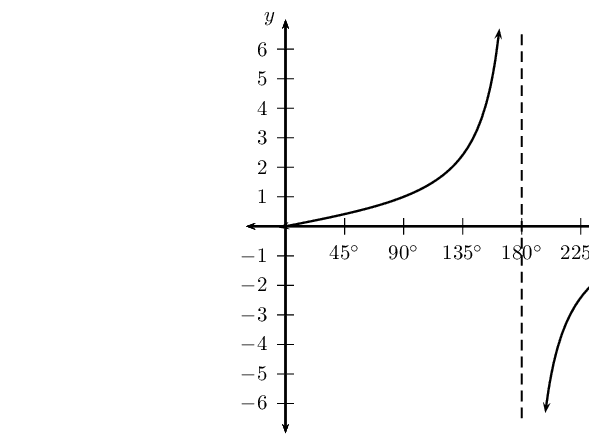
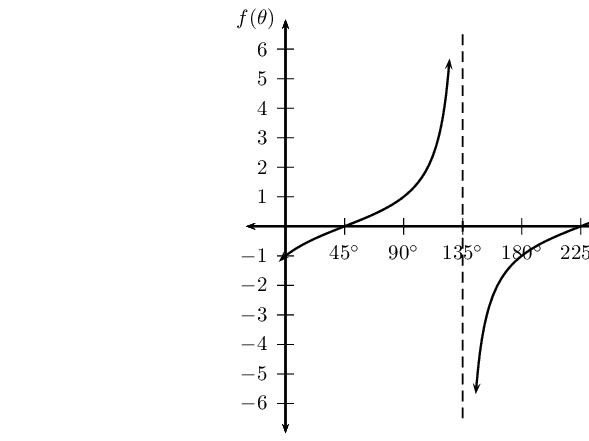
\(y = \tan \frac{1}{2}\theta\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\)
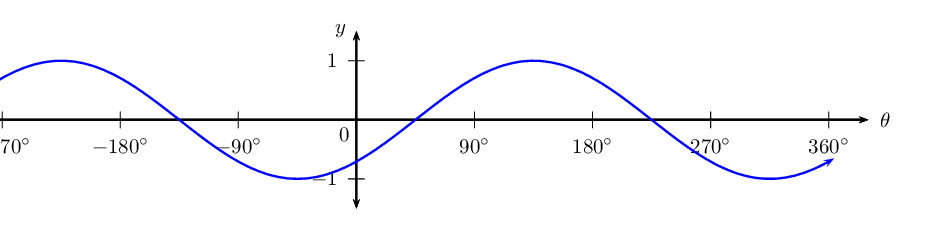
\(y = \sin (\theta-\text{45}\text{°})\) for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\)
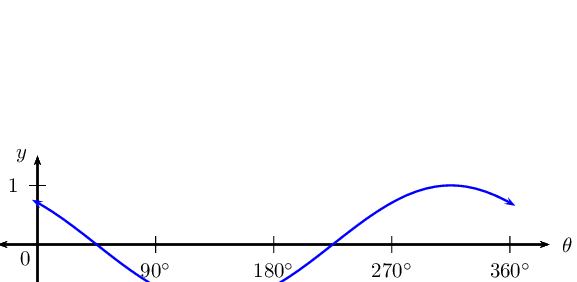
\(y = \cos (\theta+\text{45}\text{°})\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\)
\(y = \tan (\theta-\text{45}\text{°})\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\)
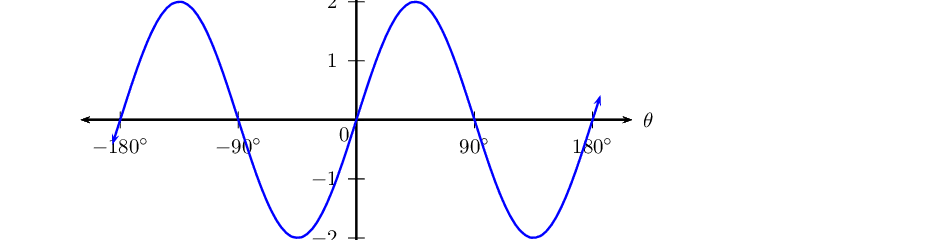
\(y = 2\sin 2\theta\) for \(-\text{180}\text{°} \leq \theta \leq \text{180}\text{°}\)
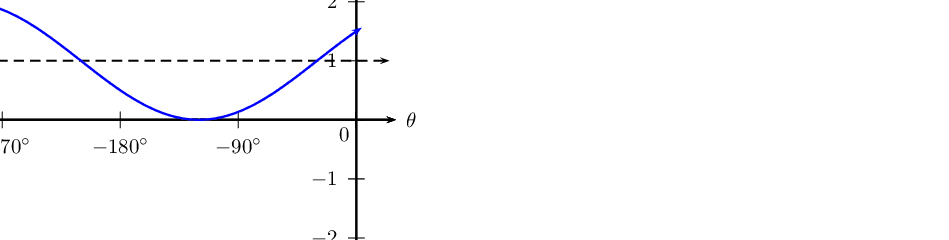
\(y = \sin (\theta+\text{30}\text{°}) + 1\) for \(-\text{360}\text{°} \leq \theta \leq \text{0}\text{°}\)
|
Previous
5.8 Summary
|
Table of Contents |
Next
6.1 Revision
|
