5.6 Summary
|
Previous
5.5 Solving cubic equations
|
Next
End of chapter exercises
|
5.6 Summary (EMCGY)
| Terminology: | |
| Expression | A term or group of terms consisting of numbers, variables and the basic operators (\(+, -, \times, \div\)). |
| Univariate expression | An expression containing only one variable. |
| Root/Zero | A root, also referred to as the “zero”, of an equation is the value of \(x\) such that \(f(x)=0\) is satisfied. |
| Polynomial |
An expression that involves one or more variables having different powers and coefficients. \(a_{n}x^{n} + \ldots + a_2x^{2} + a_{1}x + a_{0}, \text{ where } n \in \mathbb{N}_0\) |
| Monomial |
A polynomial with one term. For example, \(7a^{2}b \text{ or } 15xyz^{2}\). |
| Binomial |
A polynomial that has two terms. For example, \(2x + 5z \text{ or } 26 - g^{2}k\). |
| Trinomial |
A polynomial that has three terms. For example, \(a - b + c \text{ or } 4x^2 + 17xy - y^3\). |
| Degree/Order |
The degree, also called the order, of a univariate polynomial is the value of the highest exponent in the polynomial. For example, \(7p - 12p^2 + 3p^5 + 8\) has a degree of \(\text{5}\). |
-
Quadratic formula: \(x = \frac{-b±\sqrt{{b}^{2}-4ac}}{2a}\)
-
Remainder theorem: a polynomial \(p(x)\) divided by \(cx - d\) gives a remainder of \(p\left(\dfrac{d}{c}\right)\).
-
Factor theorem: if the polynomial \(p(x)\) is divided by \(cx - d\) and the remainder, \(p \left( \frac{d}{c} \right)\), is equal to zero, then \(cx - d\) is a factor of \(p(x)\).
-
Converse of the factor theorem: if \(cx - d\) is a factor of \(p(x)\), then \(p \left( \frac{d}{c} \right) = 0\).
-
Synthetic division:
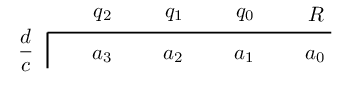
We determine the coefficients of the quotient by calculating:
\begin{align*} q_{2} &= a_{3} + \left( q_{3} \times \frac{d}{c} \right) \\ &= a_{3} \quad \text{ (since } q_{3} = 0) \\ q_{1} &= a_{2} + \left( q_{2} \times \frac{d}{c} \right) \\ q_{0} &= a_{1} + \left( q_{1} \times \frac{d}{c} \right) \\ R &= a_{0} + \left( q_{0} \times \frac{d}{c} \right) \end{align*}
|
Previous
5.5 Solving cubic equations
|
Table of Contents |
Next
End of chapter exercises
|
