What value does \({\left(\frac{2}{5}\right)}^{n}\) approach
as \(n\) tends towards \(\infty\)?
\begin{align*}
S_{n} &= \frac{2}{5} + \frac{4}{25} + \frac{8}{125} + \ldots
\\
\therefore a &= \frac{2}{5} \\
\text{And } r &= \dfrac{\frac{4}{25}}{\frac{2}{5}} \\
&= \frac{2}{5} \qquad (- 1 < r < 1) \\
\text{So then } S_{\infty} &= \frac{a}{1-r} \\
&= \frac{\frac{2}{5}}{1-\frac{2}{5}} \\
&= \frac{\frac{2}{5}}{\frac{3}{5}} \\
&= \frac{2}{3}
\end{align*}
Find the sum to infinity of the geometric series
\(3+1+\frac{1}{3}+\frac{1}{9}+ \cdots\)
\begin{align*}
a &= 3 \\
r &= \frac{1}{3} \\
S_{\infty} &= \frac{a}{1 -r} \\
&= \frac{3}{1 - \frac{1}{3}} \\
&= \frac{3}{\frac{2}{3}} \\
&= \frac{9}{2}
\end{align*}
Determine for which values of \(x\), the geometric series
\(2+\frac{2}{3} \left(x+1\right)+\frac{2}{9}
{\left(x+1\right)}^{2}+ \cdots\) will converge.
\begin{align*}
a &= 2 \\
r &= \frac{\frac{2}{3} \left(x+1\right)}{2} \\
&= \frac{1}{3} \left(x+1\right)
\end{align*}
For the series to converge, \(-1 < r < 1\), therefore:
\begin{align*}
-1&< r < 1 \\
-1 &< \frac{1}{3} \left(x+1\right) < 1 \\
-3 &< \left(x+1\right) < 3 \\
-3-1 &< x < 3-1 \\
-4 &< x < 2
\end{align*}
The sum to infinity of a geometric series with positive terms
is \(4\frac{1}{6}\) and the sum of the first two terms
is \(2\frac{2}{3}\). Find \(a\), the first term, and
\(r\), the constant ratio between consecutive terms.
\begin{align*}
T_{1} + T_{2} &= \frac{8}{3} \\
\therefore a + ar &= \frac{8}{3} \\
a(1 + r) &= \frac{8}{3} \\
\therefore a &= \frac{8}{3(1 + r)} \ldots \ldots (1) \\
S_{\infty} &= 4\frac{1}{6} = \frac{25}{6} \\
\therefore \frac{a}{1 -r}&= \frac{25}{6} \\
6a &= 25(1 -r) \ldots \ldots (2) \\
\text{Substitute eqn. } (1) \rightarrow (2): \quad 6 \left(
\frac{8}{3(1 + r)} \right)&= 25(1 -r) \\
16 &= 25(1 -r)(1 + r)\\
16 &= 25(1 - r^{2}) \\
16 &= 25 - 25r^{2} \\
25r^{2} &= 25 - 16 \\
25r^{2} &= 9 \\
r^{2} &= \frac{9}{25} \\
\therefore r &= \pm \frac{3}{5} \\
\text{But } T_{n} & > 0 \\
\therefore r &= \frac{3}{5} \\
\text{And } a &= \frac{8}{3(1 + r)} \\
&= \frac{8}{3 + 3r} \\
&= \frac{8}{3 + 3 \left(\frac{3}{5} \right)} \\
&= \frac{8}{\frac{15}{5} + \frac{9}{5}} \\
&= \frac{8}{\frac{24}{5}} \\
\therefore a &= \frac{5}{3}
\end{align*}
Use the sum to infinity to show that
\(\text{0,}\dot{\text{9}} = 1\).
Rewrite the recurring decimal:
\[\text{0,}\dot{\text{9}} = \frac{9}{10} + \frac{9}{100} + +
\frac{9}{1000} + \ldots\]
This is a geometric series with \(a = \frac{9}{10}\) and \(r
= \frac{1}{10}\).
\begin{align*}
S_{\infty} &= \frac{a}{1 - r} \\
&= \frac{\frac{9}{10}}{1 - \frac{1}{10}} \\
&= \frac{\frac{9}{10}}{\frac{9}{10}} \\
&= 1
\end{align*}
A shrub \(\text{110}\) \(\text{cm}\) high is planted in a
garden. At the end of the first year, the shrub is
\(\text{120}\) \(\text{cm}\) tall. Thereafter the growth
of the shrub each year is half of it's growth in the
previous year. Show that the height of the shrub will
never exceed \(\text{130}\) \(\text{cm}\). Draw a graph
of the relationship between time and growth.
[IEB, Nov 2003]
Write the annual growth of the shrub as a series:
\[10 + 5 + \frac{5}{2} + \frac{5}{4} + \ldots\]
This is a geometric series with \(a = 10\) and \(r =
\frac{1}{2}\).
\begin{align*}
S_{\infty} &= \frac{a}{1 - r} \\
&= \frac{10}{1 - \frac{1}{2}} \\
&= \frac{10}{\frac{1}{2}} \\
&= 20
\end{align*}
Therefore the growth of the shrub is limited to \(\text{20}\)
\(\text{cm}\), and the maximum height of the shrub is
therefore \(\text{110}\) \(\text{cm}\) +\(\text{20}\)
\(\text{cm}\) = \(\text{130}\) \(\text{cm}\).
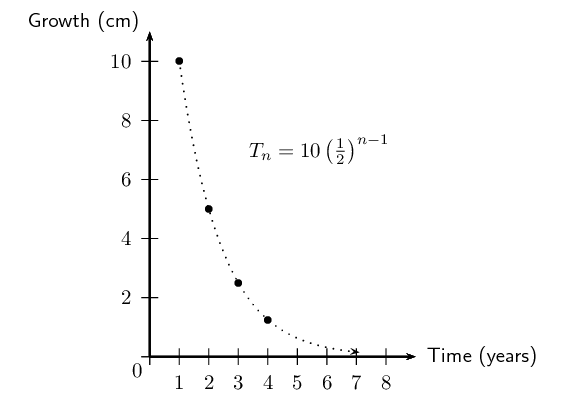
Note: we may join the points on the graph because the growth
is continuous.
Find \(p\):
\[\sum_{k = 1}^{\infty}{27p^{k}} = \sum_{t=1}^{12}{(24 - 3t)}\]
Write out the series on the RHS:
\[\sum_{t=1}^{12}{(24 - 3t)} = 21 + 18 + 15 + \ldots\]
This is an arithmetic series with \(a = 21\) and \(d = -3\).
\begin{align*}
S_{n} &= \frac{n}{2}[2a + (n - 1)d] \\
S_{12} &= \frac{12}{2}[2(21) + (12 - 1)(3)] \\
&= 6[42 - 33] \\
&= 54 \\
\therefore \sum_{t=1}^{12}{(24 - 3t)} = 54
\end{align*}
Write out the series on the LHS:
\[\sum_{k = 1}^{\infty}{27p^{k}} = 27p + 27p^{2} + 27p^{3} +
\ldots\]
This is a geometric series with \(a = 27p\) and \(r = p\)
(\(-1 < p < 1\) for the series to converge).
\begin{align*}
S_{\infty} &= \frac{a}{1 - r} \\
\therefore 54 &= \frac{27p}{1 - p} \\
27p &= 54 - 54 p \\
81 p &= 54 \\
\therefore p &= \frac{54}{81} \\
&= \frac{2}{3}
\end{align*}

