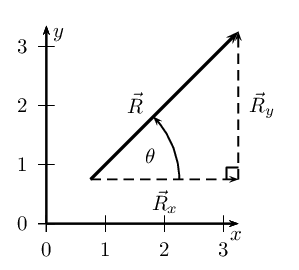
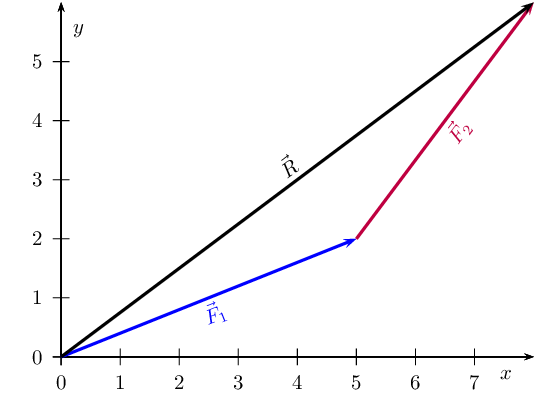
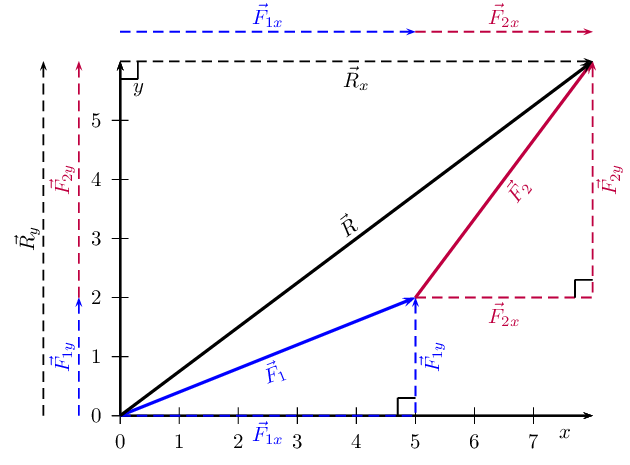
Components can also be used to find the resultant of vectors. This technique can be applied to both graphical
and algebraic methods of finding the resultant. The method is straightforward:
We can see that:
\begin{align*}
\vec{F}_1 &= \vec{F}_{1x} + \vec{F}_{1y} \\
\vec{F}_2 &= \vec{F}_{2x} + \vec{F}_{2y} \\
\vec{R} &= \vec{R}_x + \vec{R}_y
\end{align*}
\begin{align*}
\text{But,}\ \vec{R}_x &= \vec{F}_{1x} + \vec{F}_{2x} \\
\text{and}\ \vec{R}_y &= \vec{F}_{1y} + \vec{F}_{2y}
\end{align*}
In summary, addition of the \(x\)-components of the two original
vectors gives the \(x\)-component of the resultant. The same applies to
the \(y\)-components. So if we just added all the components
together we would get the same answer! This is another important
property of vectors.
Worked example 14: Adding vectors using components
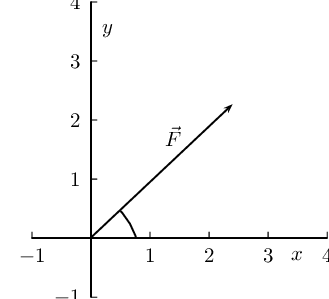
If in Figure 1.6,
\(\vec{F}_1\)=\(\text{5,385}\) \(\text{N}\) at an angle of \(\text{21,8}\)\(\text{°}\) to the
horizontal and \(\vec{F}_2\)=\(\text{5}\) \(\text{N}\) at an angle of \(\text{53,13}\)\(\text{°}\) to
the horizontal, find the resultant force, \(\vec{R}\).
Decide how to tackle the problem
The first thing we must realise is that the order that we add the vectors does not matter. Therefore, we
can work through the vectors to be added in any order. We also draw up the following table to help us work
through the problem:
|
Vector
|
\(x\)-component
|
\(y\)-component
|
Total
|
| \(\vec{F}_1\) |
|
|
|
| \(\vec{F}_2\) |
|
|
|
| Resultant |
|
|
|
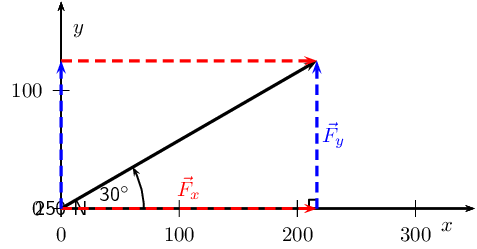
Resolve \(\vec{F}_1\) into components
We find the components of \(\vec{F}_1\) by using known trigonometric ratios. First we find the magnitude of
the vertical component, \({F}_{\mathrm{1y}}\):
\begin{align*}
\sin(\theta) &= \frac{F_{1y}}{F_1} \\
\sin(\text{21,8}\text{°}) &= \frac{F_{1y}}{\text{5,385}} \\
F_{1y} &= \left(\sin(\text{21,8}\text{°})\right)\left( \text{5,385}\right) \\
&= \text{2,00}\text{ N}
\end{align*}
Secondly we find the magnitude of the horizontal component, \({F}_{\mathrm{1x}}\):
\begin{align*}
\cos(\theta) &= \frac{F_{1x}}{F_1} \\
\cos(\text{21,8}\text{°}) &= \frac{F_{1x}}{\text{5,385}} \\
F_{1x} &= \left(\cos(\text{21,8}\text{°})\right)\left( \text{5,385} \right) \\
&= \text{5,00}\text{ N}
\end{align*}

The components give the sides of the right angle triangle, for which the original vector, \(\vec{F}_1\), is
the hypotenuse.
|
Vector
|
\(x\)-component
|
\(y\)-component
|
Resultant
|
| \(\vec{F}_1\) |
\(\text{5,00}\) \(\text{N}\) |
\(\text{2,00}\) \(\text{N}\) |
\(\text{5,385}\) \(\text{N}\) |
| \(\vec{F}_2\) |
|
|
|
| Resultant |
|
|
|
Resolve \(\vec{F}_2\) into components
We find the components of \(\vec{F}_2\) by using known trigonometric ratios. First we find the magnitude of
the vertical component, \({F}_{\mathrm{2y}}\):
\begin{align*}
\sin(\theta) &= \frac{F_{2y}}{F_2} \\
\sin( \text{53,13}\text{°}) &= \frac{F_{2y}}{5} \\
F_{2y} &= \left(\sin( \text{53,13}\text{°})\right)\left( 5\right) \\
&= \text{4,00}\text{ N}
\end{align*}
Secondly we find the magnitude of the horizontal component, \({F}_{\mathrm{2x}}\):
\begin{align*}
\cos(\theta) &= \frac{F_{2x}}{F_2} \\
\cos (\text{53,13}\text{°}) &= \frac{F_{2x}}{5} \\
F_{2x} &= \left(\cos( \text{53,13}\text{°})\right)\left( 5\right) \\
&= \text{3,00}\text{ N}
\end{align*}
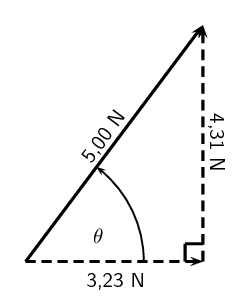
|
Vector
|
\(x\)-component
|
\(y\)-component
|
Total
|
| \(\vec{F}_1\) |
\(\text{5,00}\) \(\text{N}\) |
\(\text{2,00}\) \(\text{N}\) |
\(\text{5,385}\) \(\text{N}\) |
| \(\vec{F}_2\) |
\(\text{3,00}\) \(\text{N}\) |
\(\text{4,00}\) \(\text{N}\) |
\(\text{5}\) \(\text{N}\) |
| Resultant |
|
|
|
Determine the components of the resultant vector
Now we have all the components. If we add all the horizontal components then
we will have the \(x\)-component of the resultant vector, \({\stackrel{\to }{R}}_{x}\). Similarly, we add
all the vertical components then we will have the \(y\)-component of the resultant vector, \({\stackrel{\to
}{R}}_{y}\).
\begin{align*}
R_x &= F_{1x} + F_{2x} \\
& = \text{5,00}\text{ N} + \text{3,00}\text{ N} \\
&= \text{8,00}\text{ N}
\end{align*}
Therefore, \({\stackrel{\to }{R}}_{x}\) is \(\text{8}\) \(\text{N}\) to the right.
\begin{align*}
R_y &= F_{1y} + F_{2y} \\
& = \text{2,00}\text{ N} + \text{4,00}\text{ N} \\
&= \text{6,00}\text{ N}
\end{align*}
Therefore, \({\stackrel{\to }{R}}_{y}\) is \(\text{6}\) \(\text{N}\) up.
|
Vector
|
\(x\)-component
|
\(y\)-component
|
Total
|
| \(\vec{F}_1\) |
\(\text{5,00}\) \(\text{N}\) |
\(\text{2,00}\) \(\text{N}\) |
\(\text{5,385}\) \(\text{N}\) |
| \(\vec{F}_2\) |
\(\text{3,00}\) \(\text{N}\) |
\(\text{4,00}\) \(\text{N}\) |
\(\text{5}\) \(\text{N}\) |
| Resultant |
\(\text{8,00}\) \(\text{N}\) |
\(\text{6,00}\) \(\text{N}\) |
|
Determine the magnitude and direction of the resultant vector
Now that we have the components of the resultant, we can use the Theorem of Pythagoras to determine the
magnitude of the resultant, R.
\begin{align*}
R^2 &= (R_y)^2 + (R_x)^2 \\
& = (\text{6,00})^2 + (\text{8,00})^2 \\
&= \text{100,00}\\
R &= \text{10,00}\text{ N}
\end{align*}
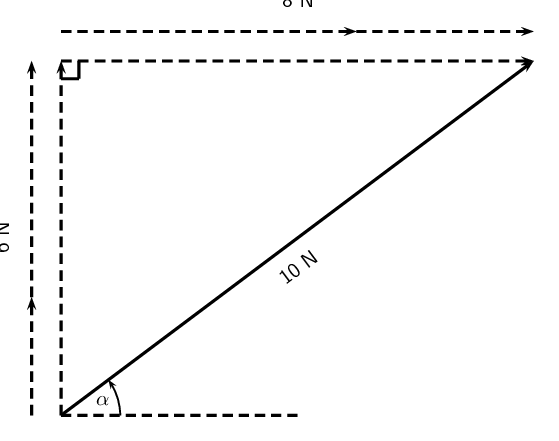
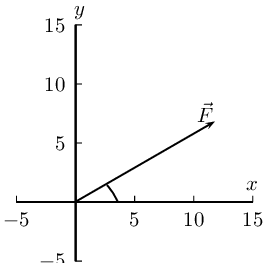
The magnitude of the resultant, R is \(\text{10,00}\) \(\text{N}\). So all we have to do is calculate its
direction. We can specify the direction as the angle the vectors makes with a known direction. To do this
you only need to visualise the vector as starting at the origin of a coordinate system. We have drawn this
explicitly below and the angle we will calculate is labelled α.
Using our known trigonometric ratios we can calculate the value of \(\alpha\):
\begin{align*}
\tan\alpha &= \frac{\text{6,00}}{\text{8,00}}\\
\alpha &= \tan^{-1}\frac{\text{6,00}}{\text{8,00}}\\
\alpha &= \text{36,9}\text{°}
\end{align*}
Quote the final answer
\(\stackrel{\to }{R}\) is \(\text{10}\) \(\text{N}\) at an angle of \(36,{9}^{°}\) to the positive
\(x\)-axis.
Worked example 15: Resultant using components
Determine, by resolving into components, the resultant of the following four forces acting at a point:
- \(\vec{F}_1\)=\(\text{3,5}\) \(\text{N}\) at \(\text{45}\)\(\text{°}\) to the positive \(x\)-axis.
- \(\vec{F}_2\)=\(\text{2,7}\) \(\text{N}\) at \(\text{63}\)\(\text{°}\) to the positive \(x\)-axis.
- \(\vec{F}_3\)=\(\text{1,3}\) \(\text{N}\) at \(\text{127}\)\(\text{°}\) to the positive \(x\)-axis.
- \(\vec{F}_4\)=\(\text{2,5}\) \(\text{N}\) at \(\text{245}\)\(\text{°}\) to the positive \(x\)-axis.
Sketch the problem
Draw all of the vectors on the Cartesian plane. This does not have to be precisely accurate because we are
solving algebraically but vectors need to be drawn in the correct quadrant and with the correct relative
positioning to each other.
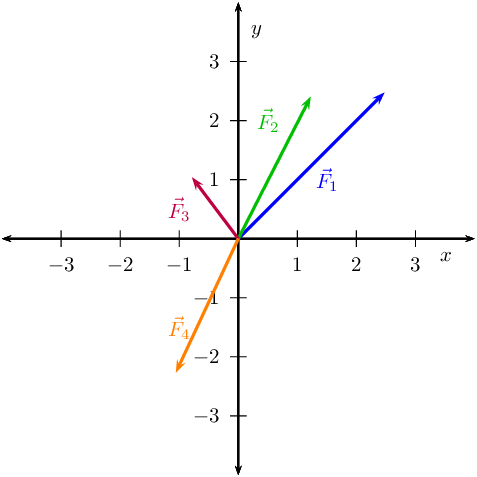
We are going to record the various components in a table to help us manage keep track of the calculation.
For each vector we need to determine the components in the \(x\)- and \(y\)-directions.
|
Vector
|
\(x\)-component
|
\(y\)-component
|
Total
|
| \(\vec{F}_1\) |
|
|
\(\text{3,5}\) \(\text{N}\) |
| \(\vec{F}_2\) |
|
|
\(\text{2,7}\) \(\text{N}\) |
| \(\vec{F}_3\) |
|
|
\(\text{1,3}\) \(\text{N}\) |
| \(\vec{F}_4\) |
|
|
\(\text{2,5}\) \(\text{N}\) |
| \(\vec{R}\) |
|
|
|
Determine components of \(\vec{F}_1\)

\begin{align*}
\sin(\theta) &= \frac{F_{1y}}{F_1} \\
\sin( \text{45}\text{°}) &= \frac{F_{1y}}{\text{3,5}} \\
F_{1y} &= \left(\sin (\text{45}\text{°})\right)\left( \text{3,5}\right) \\
&= \text{2,47}\text{ N}
\end{align*}
Secondly we find the magnitude of the horizontal component, \({F}_{\mathrm{1x}}\):
\begin{align*}
\cos(\theta) &= \frac{F_{1x}}{F_1} \\
\cos( \text{45}\text{°}) &= \frac{F_{1x}}{\text{3,5}} \\
F_{1x} &= \left(\cos (\text{45}\text{°})\right)\left( \text{3,5}\right) \\
&= \text{2,47}\text{ N}
\end{align*}
Determine components of \(\vec{F}_2\)

\begin{align*}
\sin(\theta) &= \frac{F_{2y}}{F_2} \\
\sin(\text{63}\text{°}) &= \frac{F_{2y}}{\text{2,7}} \\
F_{2y} &= \left(\sin(\text{63}\text{°})\right)\left( \text{2,7}\right) \\
&= \text{2,41}\text{ N}
\end{align*}
Secondly we find the magnitude of the horizontal component, \({F}_{\mathrm{2x}}\):
\begin{align*}
\cos\theta &= \frac{F_{2x}}{F_2} \\
\cos( \text{63}\text{°}) &= \frac{F_{2x}}{\text{2,7}} \\
F_{2x} &= \left(\cos(\text{63}\text{°})\right)\left( \text{2,7}\right) \\
&= \text{1,23}\text{ N}
\end{align*}
Determine components of \(\vec{F}_3\)

\begin{align*}
\sin(\theta) &= \frac{F_{3y}}{F_3} \\
\sin( \text{127}\text{°}) &= \frac{F_{3y}}{\text{1,3}} \\
F_{3y} &= \left(\sin \text{127}\text{°}\right)\left( \text{1,3}\right) \\
&= \text{1,04}\text{ N}
\end{align*}
Secondly we find the magnitude of the horizontal component, \({F}_{\mathrm{3x}}\):
\begin{align*}
\cos(\theta) &= \frac{F_{3x}}{F_3} \\
\cos (\text{127}\text{°}) &= \frac{F_{3x}}{\text{1,3}} \\
F_{3x} &= \left(\cos \text{127}\text{°}\right)\left( \text{1,3}\right) \\
&= -\text{0,78}\text{ N}
\end{align*}
Determine components of \(\vec{F}_4\)

\begin{align*}
\sin(\theta) &= \frac{F_{4y}}{F_4} \\
\sin( \text{245}\text{°}) &= \frac{F_{4y}}{\text{2,5}} \\
F_{4y} &= \left(\sin( \text{245}\text{°})\right)\left( \text{2,5}\right) \\
&= -\text{2,27}\text{ N}
\end{align*}
Secondly we find the magnitude of the horizontal component, \({F}_{\mathrm{4x}}\):
\begin{align*}
\cos(\theta) &= \frac{F_{4x}}{F_4} \\
\cos( \text{245}\text{°}) &= \frac{F_{4x}}{\text{2,5}} \\
F_{4x} &= \left(\cos( \text{245}\text{°})\right)\left( \text{2,5}\right) \\
&= -\text{1,06}\text{ N}
\end{align*}
Determine components of resultant
Sum the various component columns to determine the components of the resultant. Remember that if the
component was negative don't leave out the negative sign in the summation.
|
Vector
|
\(x\)-component
|
\(y\)-component
|
Total
|
| \(\vec{F}_1\) |
\(\text{2,47}\) \(\text{N}\) |
\(\text{2,47}\) \(\text{N}\) |
\(\text{3,5}\) \(\text{N}\) |
| \(\vec{F}_2\) |
\(\text{1,23}\) \(\text{N}\) |
\(\text{2,41}\) \(\text{N}\) |
\(\text{2,7}\) \(\text{N}\) |
| \(\vec{F}_3\) |
\(-\text{0,78}\) \(\text{N}\) |
\(\text{1,04}\) \(\text{N}\) |
\(\text{1,3}\) \(\text{N}\) |
| \(\vec{F}_4\) |
\(-\text{1,06}\) \(\text{N}\) |
\(-\text{2,27}\) \(\text{N}\) |
\(\text{2,5}\) \(\text{N}\) |
| \(\vec{R}\) |
\(\text{1,86}\) \(\text{N}\) |
\(\text{3,65}\) \(\text{N}\) |
|
Now that we have the components of the resultant, we can use the Theorem of Pythagoras to determine the
magnitude of the resultant, R.
\begin{align*}
R^2 &= (R_y)^2 + (R_x)^2 \\
& = (\text{1,86})^2 + (\text{3,65})^2 \\
&= \text{16,78}\\
R &= \text{4,10}\text{ N}
\end{align*}
We can also determine the angle with the positive \(x\)-axis.
\begin{align*}
\tan(\alpha) &= \frac{\text{1,86}}{\text{3,65}}\\
\alpha &= \tan^{-1}(\frac{\text{3,65}}{\text{1,86}})\\
\alpha &= \text{27,00}\text{°}
\end{align*}
Quote the final answer
The resultant has a magnitude of \(\text{4,10}\) \(\text{N}\) at and angle of
\(\text{27,00}\)\(\text{°}\) to the positive \(x\)-direction.