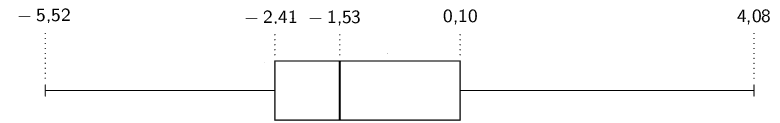\(-\text{3,4}\) ; \(-\text{3,1}\) ; \(-\text{6,1}\) ;
\(-\text{1,5}\) ; \(-\text{7,8}\) ; \(-\text{3,4}\) ;
\(-\text{2,7}\) ; \(-\text{6,2}\)
Mean:
\begin{align*}
\overline{x}
&= \frac{(-\text{3,4}) + (-\text{3,1}) +
(-\text{6,1}) + (-\text{1,5}) + (-\text{7,8}) +
(-\text{3,4}) + (-\text{2,7}) + (-\text{6,2})}{8} \\
&\approx -\text{4,3}
\end{align*}
To compute the quartiles, we order the data:
\(-\text{7,8}\) ; \(-\text{6,2}\) ; \(-\text{6,1}\) ;
\(-\text{3,4}\) ; \(-\text{3,4}\) ; \(-\text{3,1}\) ;
\(-\text{2,7}\) ; \(-\text{1,5}\)
We use the diagram below to find at or between which values
the quartiles lie.
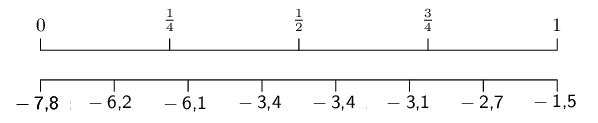
For the first quartile the position is between the second and
third values.
The second value is \(-\text{6,2}\) and the third value
is \(-\text{6,1}\), which means that the first quartile
is \(\frac{-\text{6,2} - \text{6,1}}{2}=-\text{6,15}\).
For the median (second quartile) the position is halfway
between the fourth and fifth values.
Since both these values are \(-\text{3,4}\), the median
is \(-\text{3,4}\).
For the third quartile the position is between the sixth and
seventh values.
Therefore the third quartile is \(-\text{2,9}\).
\(-\text{6}\) ; \(-\text{99}\) ; \(\text{90}\) ;
\(\text{81}\) ; \(\text{13}\) ; \(-\text{85}\) ;
\(-\text{60}\) ; \(\text{65}\) ; \(-\text{49}\)
Mean:
\begin{align*}
\overline{x}
&= \frac{(-\text{6}) + (-\text{99}) + (\text{90}) +
(\text{81}) + (\text{13}) + (-\text{85}) + (-\text{60})
+ (\text{65}) + (-\text{49})}{9} \\
&\approx -\text{5,6}
\end{align*}
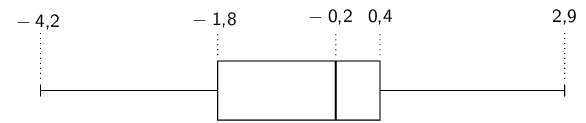
To compute the quartiles, we order the data:
\(-\text{99}\) ; \(-\text{85}\) ; \(-\text{60}\) ;
\(-\text{49}\) ; \(-\text{6}\) ; \(\text{13}\) ;
\(\text{65}\) ; \(\text{81}\) ; \(\text{90}\)
We use the diagram below to find at or between which values
the quartiles lie.

We see that the quartiles are at \(-\text{60}\);
\(-\text{6}\); and \(\text{65}\).
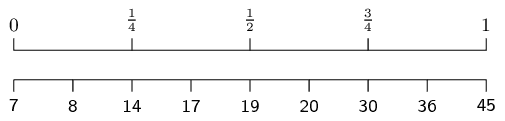
\(\text{7}\) ; \(\text{45}\) ; \(\text{11}\) ; \(\text{3}\) ;
\(\text{9}\) ; \(\text{35}\) ; \(\text{31}\) ;
\(\text{7}\) ; \(\text{16}\) ; \(\text{40}\) ;
\(\text{12}\) ; \(\text{6}\)
The mean is \(\overline{x} = \text{18,5}\).
To compute the quartiles, we order the data:
\[3\ ;\ 6\ ;\ 7\ ;\ 7\ ;\ 9\ ;\ 11\ ;\ 12\ ;\ 16\ ;\ 31\ ;\ 35\
;\ 40\ ;\ 45\]
We use the diagram below to find at or between which values
the quartiles lie.
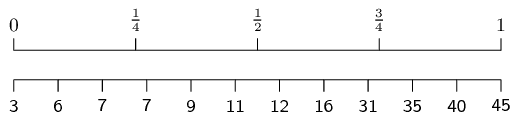
For the first quartile the position is between the third and
fourth values.
Since both these values are equal to \(\text{7}\), the
first quartile is \(\text{7}\).
For the median (second quartile) the position is halfway
between the sixth and seventh values.
The sixth value is \(\text{11}\) and the seventh value
is \(\text{12}\), which means that the median is
\(\frac{11+12}{2}=\text{11,5}\).
For the third quartile the position is between the ninth and
tenth values.
Therefore the third quartile is \(\frac{31+35}{2}=33\).